DFT

Poznato je da se svaki periodičan ili aperiodičan signal može razložiti na sumu sinusoidalnih komponenti čije se učestanosti razlikuju ili za konačan iznos kao što je to slučaj kod periodičnih signala ili za beskonačno mali iznos kao kod aperiodičnih signala. Postupak izdvajanja harmonijskih komponenti iz složenog signala se naziva i spektralna ili harmonijska analiza signala. Diskretna Furijeova transformacija (DFT) obavlja prebacivanje signala iz vremenskog u spektralni domen. Primena Diskretne Furijeove transformacije u digitalnoj obradi signala je velika. Pre svega, DFT se koristi kao neophodan alat u spektralnoj analizi signala. DFT omogućava efikasno izvođenje filtriranja u frekvencijskom domenu. Značaj Diskretne Furijeove transformacije u digitalnoj obradi signala potiče od toga što postoje veoma efikasni algoritmi za izračunavanje DFT.

Realni i imaginarni deo spektralnih komponenti se izračunava po formulama:

$Re(X_k)=\sum_{i=0}^{N-1}x_i cos\left(\frac{2\pi ki}{N}\right),$

$Im(X_k)=-\sum_{i=0}^{N-1}x_i sin\left(\frac{2\pi ki}{N}\right)$

Gde su $x_i$ odbirci signala za koje se izračunava DFT.

Za uzorke DFT-a moguće je izračunati amplitudu $|X_k|$ i fazu $arg(X_k)$ koji predstavljaju amplitudnu i faznu karakteristiku prema sledecim izrazima:

$|X_k|=\sqrt{Re(X_k)^2+Im(X_k)^2}$

$arg(X_k)=atan2(Im(X_k),Re(X_k))$

gdje je sa atan2 označena 4-kvadrantna arctg funkcija od imaginarnog i realnog dela kompleksnih uzoraka DFT-a $X_k$ .

Zadaci

Zadatak 1

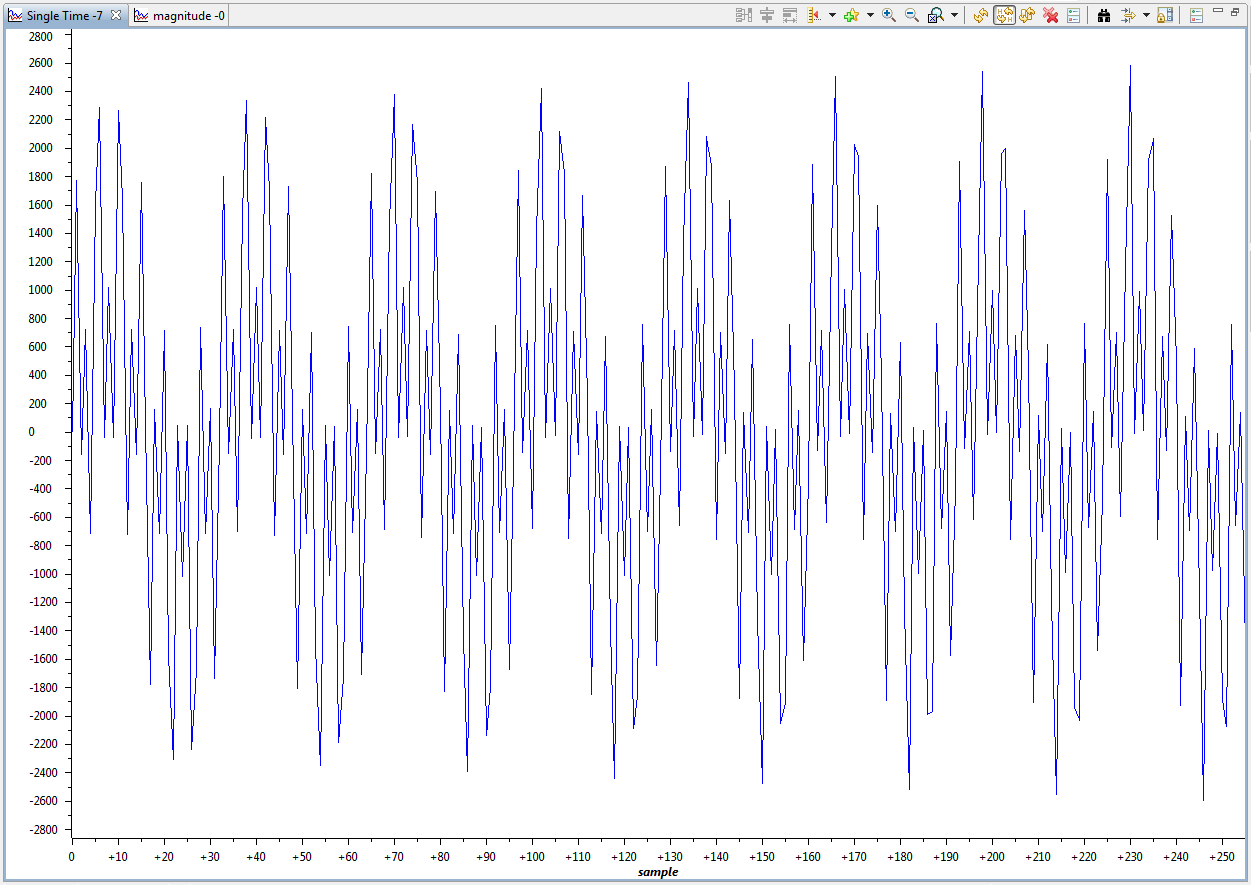
Za zadati signal odrediti:

Od koliko sinusoidalnih signala se sastoji zadati slozeni signal?
Koje su frekvencije svake komponente ovog slozenog signala?
Koji podatak nedostaje kako bi to mogli da odredite?

int signal[DUZINA_BAFERA] = {
     0,  1771,  -163,   721,  -721,  1608,  2288,   -47,  1022,   -46,  2266, 1638,
  -728,   720,  -163,  1757,    33, -1783,   161,  -722,   716, -1576, -2313,   49,
 -1022,    46, -2242, -1670,   734,  -719,   164, -1742,   -67,  1798,
  -160,   722,  -709,  1545,  2335,   -49,  1021,   -44,  2218,  1701,  -738,
   718,  -165,  1728,   101, -1810,   158,  -722,   703, -1513, -2358,    47,
 -1020,    42, -2194, -1730,   743,  -715,   163, -1713,  -135,  1823,  -156,
   721,  -694,  1481,  2380,   -48,  1018,   -40,  2169,  1761,  -747,   713,
  -163,  1697,   170, -1835,   154,  -721,   687, -1449, -2401,    47, -1016,
    36, -2144, -1792,   751,  -711,   162, -1682,  -203,  1846,  -150,   719,
  -678,  1418,  2423,   -45,  1014,   -33,  2120,  1822,  -753,   707,  -162,
  1665,   237, -1858,   147,  -718,   672, -1385, -2444,    43, -1012,    30,
 -2094, -1852,   756,  -704,   159, -1650,  -272,  1868,  -143,   717,  -662,
  1353,  2464,   -41,  1010,   -27,  2070,  1880,  -758,   700,  -157,  1633,
   305, -1880,   139,  -714,   654, -1322, -2485,    38, -1007,    22, -2044,
 -1910,   760,  -696,   154, -1616,  -339,  1889,  -134,   713,  -644,  1290,
  2504,   -35,  1004,   -18,  2018,  1939,  -762,   692,  -152,  1599,   372,
 -1898,   130,  -710,   634, -1257, -2525,    32, -1001,    12, -1992, -1969,
   763,  -688,   149, -1580,  -406,  1907,  -124,   707,  -624,  1225,  2544,
   -27,   996,    -6,  1965,  1996,  -764,   683,  -146,  1563,   440, -1915,
   119,  -704,   614, -1192, -2562,    23,  -993,     1, -1939, -2025,   763,
  -677,   142, -1545,  -473,  1924,  -113,   700,  -603,  1159,  2581,   -19,
   989,     3,  1913,  2052,  -763,   672,  -138,  1527,   506, -1931,   107,
  -697,   592, -1127, -2600,    13,  -984,   -10, -1886, -2080,   761,  -666,
   135, -1508
};

Pomoc

Najjednostavniji nacin da se u CCS vidi signal u frekventnom domenu je da se prikaze njegov "FFT Magnitude Graph".

Zadatak 2

Implementirati funkciju dft(), koja ce izracunati sve spektralne komponente signala. Brzina odabiranja signala je 8kHz.

Iskoristiti funkciju dft() i prikazati samo one spektralne komponente koje postoje. Koje su njihove frekvencije i koliko ih ima?

Resenje

#include <math.h>

#define DUZINA_BAFERA 256

int Mag [DUZINA_BAFERA/2];
int sinus[DUZINA_BAFERA];
int cosinus[DUZINA_BAFERA];
int signal[DUZINA_BAFERA];

void trigLookup(int sinus[], int cosinus[], int duzina) {
    int i;
    for(i=0; i<duzina; i++){
        sinus[i]=(int)(sin(6.28*i/duzina)*32767);  // Q15
        cosinus[i]=(int)(cos(6.28*i/duzina)*32767);  // Q15
    }
}

void dft(int x[], int N) {
    int i, k;
    long xRe, xIm;
    for (k=0; k<(N/2); k++) {
        xRe=0;
        xIm=0;
        for(i=0; i<N; i++){
            xRe += ((long)x[i]*(long)cosinus[(k*i)%N])>>15;
            xIm += ((long)x[i]*(long)sinus[(k*i)%N])>>15;
        }
        Mag[k]=(((long)(xRe>>7)*(long)(xRe>>7))+((long)(xIm>>7)*(long)(xIm>>7)))>>11;
    }
}

void main(void) {
    int i;

    // Generisi lookup tabele za sin i cos
    trigLookup(sinus, cosinus, DUZINA_BAFERA);

    // Uradi DFT signala. Spektralne komponente se nalaze u vektoru Mag[]
    dft(signal, DUZINA_BAFERA);

    // Odredi sve frekvencije koje se pojavljuju u signalu
    /*
     *  Ovde ubaciti kod
     */

    while(1);
}

Zadatak 3*

Koriscenjem FIR filtera, odvojiti svaku komponentu signala ponaosob.

DFT

DFT