Lookup tabela

Lookup (lukap) tabela je tabela indeksiranih vrednosti neke funkcije. U C jeziku se najčešče realizuje kao niz. Napredni jezici kao Python-a, uvode strukturu podataka dictionary, koja je veoma sličan lookup tabelama. Lookup tabele se, između ostalog, koriste kako bi se skratilo vreme izračunavanja funkcije. Umesto da se vrednost funkcije računa, korišćenjem lookup tabele "pogleda" se vrednost funkcije y=f(x) koja je, zapravo, vrednost elementa niza sa indeksom x. Za sve vrednosti za koje ne postoji x može se vršiti neka vrsta interpolacije, najčešće linearna. Tablica množenja je primer lookup tabele, a logaritamske i triginometrijske tablice, kojih se verovatno seća generacija vaših roditelja, su još jedan primer lookup tabela.

Postoji nekoliko ograničenja lookup tabela i to su:

1. Količina raspoložive memorije; Memorija je svakako ograničena, negde više, negde manje, a samim tim je veličina lookup tabele ograničena. Količina memorije direktno utiče na preciznost funkcije koja koristi lookup tabelu.
2. Preciznost; Ukoliko nema tražene vrednosti funkcije u tabeli, najčešće se ili kao rezultat vraća najbliža vrednost, ili se nekim vidom interpolacije dolazi do približne vrednosti funkcije.
3. Vreme potrebno za generisanje tabele; Lookup tabela se mora na neki način generisati, najčešće pri inicijalizaciji programa. Vreme se može uštedeti tako što će lookup tabela biti hardkodovana u program ili u Boot ROM, kao što je to slučaj kod Texas Instrumentsovih DSP-jeva. Boot ROM reference guide je dokument u kome se može videti kako izgleda Boot ROM i u kom delu se nalaze lookup tabele. Tabele u Boot ROM-u su jedna od specifičnosti digitalnih signal procesora.

Pogledajmo primer funkcije y=sin(x). Ova funkcija se obično računa CORDIC algoritmom ili razvijanjem u Tejlorov polinom. Ako je razvijemo u Tejlorov polinom dobićemo:

$sin(x) \approx x- \frac{x^{3}}{3!} + \frac{x^{5}}{5!} - \frac{x^{7}}{7!} \approx x- \frac{x^{3}}{6} + \frac{x^{5}}{120} - \frac{x^{7}}{5040}$

C funkcija koja na ovaj način računa sin(x) bi izgledala ovako:

float tsin(float x) {
    return x-((x*x*x)/6)+((x*x*x*x*x)/120)-((x*x*x*x*x*x*x)/5040);
}

Kao što se vidi iz koda, funkcija ima:

• dve operacije sabiranja,
• dve operacije oduzimanja,
• tri operacije deljenja (veoma "skupo" što se tiče procesorskog vremena) i
• dvanaest operacija množenja ("skupo").

Vreme računanja ove funkcije, mereno na F28335 DSP-u, je 2564 ciklusa (taktova kloka).

Ako sin(x) izračunamo koristeći lookup tabele C funkcijom koja izgleda ovako:

float lsin(float x) {
    int i,y;
    i=(int)((x/_2PI)*DUZINA);  // racuna indeks, t=396
    y=sinLookupTable[i];  // uzima Q15 vrednost, t=13
    return (float)y/32767.;  // uzima vrednost iz tabele, t=319
}

Iz koda se vidi da imamo dva deljenja i jedno množenje. Ovakvo "računanje" sin(x) je trajalo 728 ciklusa. U ovoj funkciji se najviše vremena gubilo u prevođenju između fixed point Q15 formata u kome je data lookup tabela i float point-a u kome nam je lakše da predstavimo vrednosti. S obzirom da DSP sa kojim ćemo raditi, ne ume da radi sa float brojevima jer nema FPU, ukoliko bi sve bilo predstavljeno u fixed point Q15 formatu, sin(x) bi bio izračunat za 13 ciklusa, što je značajna ušteda u vremenu.

Iz koda se može videti da funkcija lsin() vraća vrednost za najbliže x. Funkciji se može povećati preciznost tako što će se vrednost za x koje ne postoji u tabeli računati nekim tipom interpolacije. Najjednostavnija je linearna interpolacija.

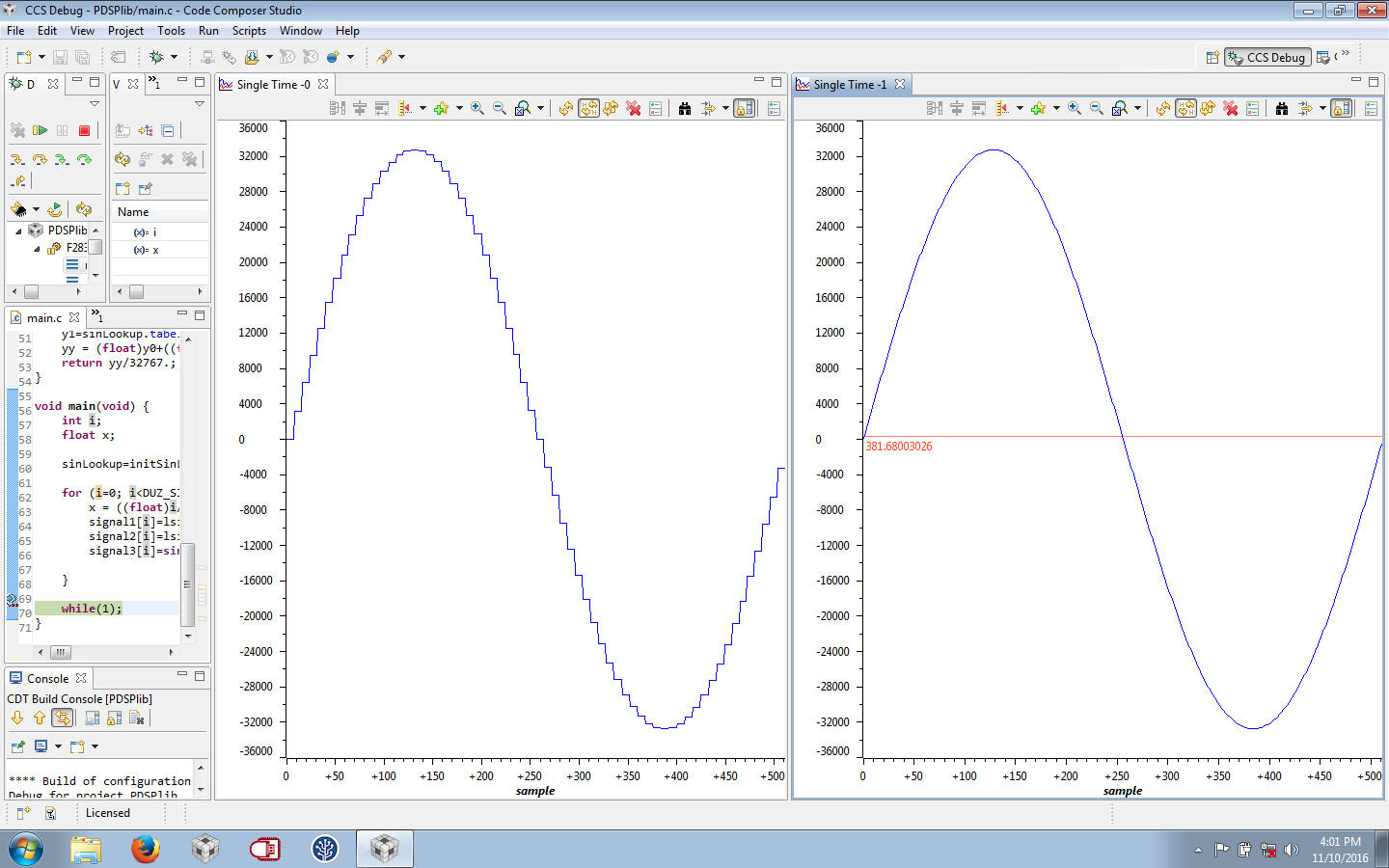
Na slici je prikazana razlika između funkcije koja ne koristi interpolaciju pri čitanju iz lookup tabela (leva sinusoida) i one koja koristi interpolaciju (desna sinusoida).